Analyzing Spatial Correlation between Purchase Power Index and Gambling Stores (2)

Theoretical framework: This GIS study applies Geographically Weighted Regression (GWR) to investigate the spatial relationship between Purchasing Power Index (PPI) and the distribution of gambling-related retail establishments within the city of Madrid. My aim is to account for spatially varying relationships driven by local urban contexts, under the assumption that the relationship between socioeconomic conditions and the presence of gambling venues varies across urban space and his socioeconomic patterns. My hypothesis is that this socioeconomic conditions of the urban fabric I mention, can be a breeding ground for the location of Betting Shops/Gambling Stores (AKA bookmaker in UK or bookie in the US), or in other words, I am attempting to Detect Urban Vulnerability to Gambling Harm.

I have chosen this Purchasing Power Index (PPI) as it’s a standardized socioeconomic indicator that represents the relative capacity of households to spend and consume goods and services within a given geographic area. It typically integrates information on income levels, employment, and demographic structure, and is expressed as a relative measure rather than an absolute monetary value, allowing comparisons across spatial units such as census sections. The logic says: The higher the PPI, the lower the vulnerability (where ) thus the more likely to find Gambling Stores around.

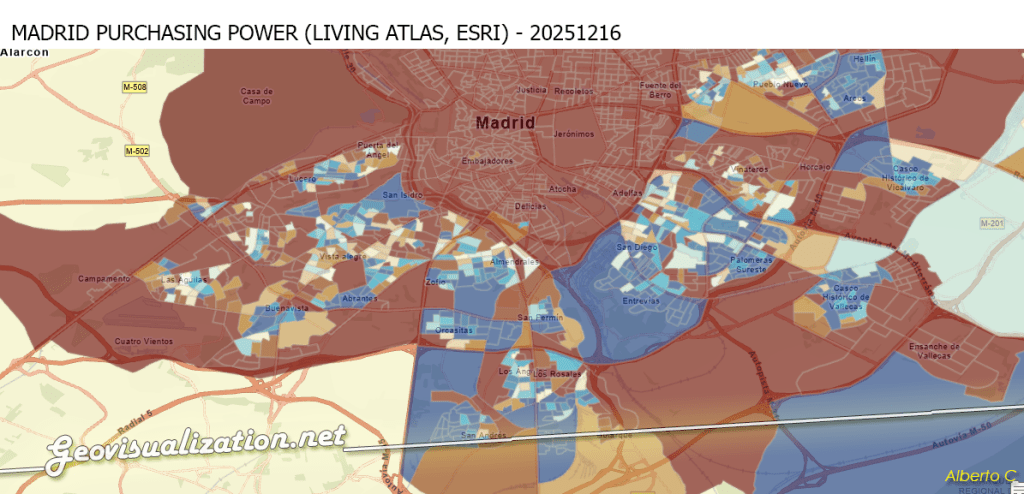
A potential relationship between purchasing power and the location of Gambling Stores arises from commercial location strategies and socioeconomic vulnerability dynamics. Gambling operators may preferentially locate in areas where household purchasing power and consumption patterns maximize demand, or conversely in areas with lower purchasing power where gambling expenditure may function as a substitute consumption behavior. As a result, the spatial distribution of gambling establishments may reflect underlying socioeconomic gradients within the urban fabric.

From a spatial analysis perspective, traditional global regression models (e.g., Ordinary Least Squares) impose a single, spatially invariant relationship across the entire study area. However, urban socioeconomic processes are inherently heterogeneous, especially in large metropolitan areas such as Madrid, where neighborhood-level dynamics, urban morphology, and socioeconomic gradients differ significantly between districts. GWR is therefore selected as the most appropriate method to capture local variations in model coefficients and to provide geographically explicit insights.

Sources: The analysis integrates two primary datasets, both harmonized at the census section level (sección censal), which represents the finest administrative unit for socioeconomic statistics in Spain:

• Gambling Stores Local Census (2024):
  An official census of commercial premises provided by the City of Madrid, including the geolocated inventory of gambling-related establishments (e.g., betting shops, gaming halls). For analytical purposes, individual point locations were spatially aggregated to census sections, generating a count of Gambling Stores per census section. (–>Figura 3)
• Purchasing Power Index (INE, 2022, extracted from ESRI’s LIVING ATLAS):
  Socioeconomic data derived from the Spanish National Statistics Institute (INE), used ESRI demographics for providing a standardized Purchasing Power Index at the census section level. This indicator reflects relative household purchasing capacity and is widely used as a proxy for local socioeconomic status.

The census section is adopted as the spatial unit of analysis to ensure statistical consistency between datasets and to align with official demographic and economic reporting standards.

I used ArcMap 10.6.1 Spatial Statistics Tool /Modelling Spatial Relationships /Geographically Weighted Regression. Also visualized and geoprocessed in Global Mapper 26.2.

Geographically Weighted Regression is a local regression technique that extends classical linear regression by allowing model parameters to vary spatially. Instead of estimating a single global coefficient, GWR computes a separate regression equation for each spatial unit, calibrated using nearby observations weighted by their geographic proximity.

I would like to mention that, at this point, having fed the tool (using ArcMap 10.6.1) with the necessary inputs (dependent and explanatory variables), I am noting down the results and adding them to the article in order to systematize my understanding (and perhaps that of some of you), but my explanatory capacity is still limited. I continue thou.

Formally, the GWR model can be expressed as:$$y_i = \beta_0(u_i, v_i) + \beta_1(u_i, v_i) x_i + \varepsilon_i$$

where:

• yi​ represents the number of Gambling Stores in census section i,
• xi​ corresponds to the Purchasing Power Index,
• (ui​,vi​) are the spatial coordinates of census section i,
• β0​ and β1​ are location-specific parameters,
• εi​ is the local error term.

This formulation allows the strength and direction of the relationship between purchasing power and gambling store presence to vary across Madrid.

And these were the results/output

OBJECT_ID / VARNAME / VARIABLE / DEFINITION
1 / Bandwidth / 6563,230379
2 / Residual Squares / 513,203175
3 / Effective Number / 12,898945
4 / Sigma / 0,45955
5 / AICc / 3141,813059
6 / R² / 0,016602
7 / R² Adjusted / 0,011787
8 / Dependent Field / 0 / Join_Count (Amount of Gambling Stores in the same Census Section)
9 / Explanatory Field / 1 / PPIDX_CY (Purchase Power Index)

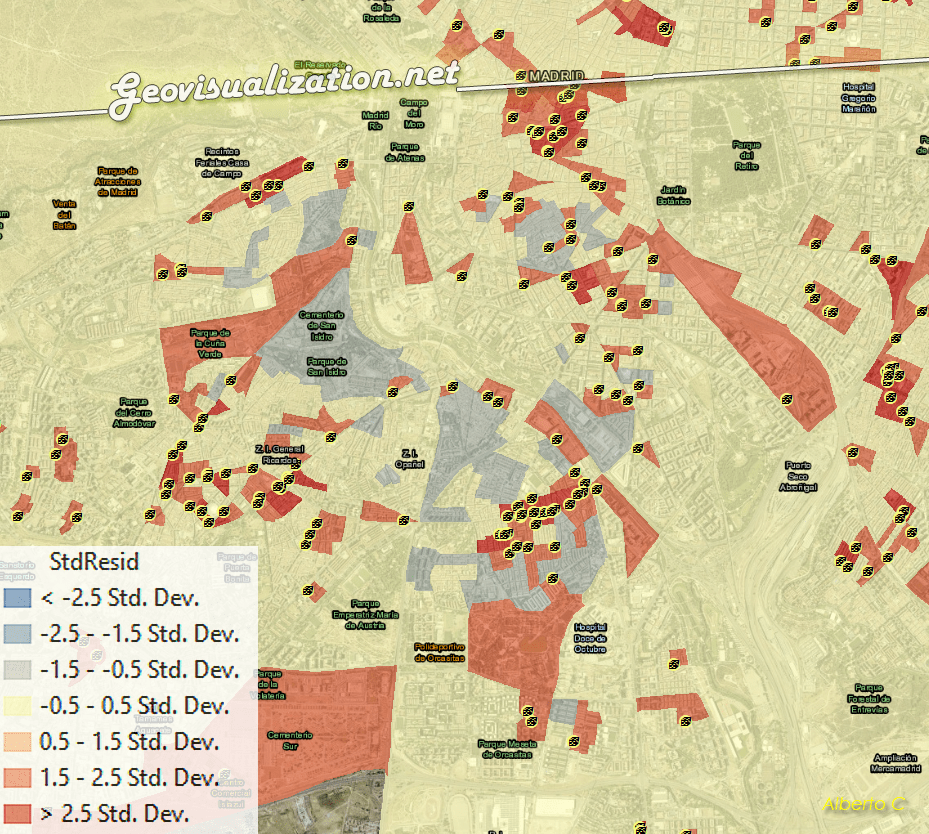
The geographically weighted regression model shows a very low explanatory power (adjusted R² = 0,011787), indicating that purchasing power alone does not meaningfully explain the spatial distribution of betting shops, even when allowing for spatially varying relationships.

A critical component of GWR is the definition of the spatial weighting scheme, which determines how neighboring census sections influence each local regression. In this analysis:

• A distance-based kernel function is used to assign higher weights to closer census sections and progressively lower weights to more distant ones.
• The bandwidth—controlling the spatial extent of each local calibration—is optimized automatically using AICc minimization, balancing model fit and complexity.

This adaptive approach ensures that densely populated urban areas benefit from a more localized calibration, while peripheral areas incorporate information from a broader neighborhood when necessary.

The GWR model produces several spatially explicit outputs of analytical relevance:

• Local regression coefficients for the Purchasing Power Index, revealing where purchasing power is more strongly or weakly associated with the presence of Gambling Stores.
• Local R² values, indicating how well the model explains variance in gambling store distribution in different parts of the city.
• Residual surfaces, used to identify spatial patterns of over- or under-prediction and potential omitted variables.

Rather than seeking a single city-wide conclusion, the emphasis is placed on geographic patterns, such as clusters of census sections where lower purchasing power is more strongly associated with higher concentrations of gambling establishments, or conversely, areas where this relationship is weak or absent.

By adopting a geographically weighted approach, this analysis explicitly acknowledges that urban socioeconomic processes are spatially contingent. The resulting maps of local coefficients provide actionable insights for urban policy, public health, and regulatory frameworks, allowing stakeholders to identify areas where gambling availability may be more closely linked to socioeconomic vulnerability.

From the standpoint of a spatial analyst, GWR serves not only as a statistical tool but as an exploratory framework that integrates spatial thinking directly into the modeling process. It enables an interpretation of the urban landscape of Madrid, grounded in official data sources and aligned with best practices in spatial econometric analysis.

Despite the analytical advantages of Geographically Weighted Regression in capturing spatial heterogeneity, several ***assumptions and limitations**** must be acknowledged to ensure a transparent and rigorous interpretation of the results.

• First, GWR assumes that spatial non-stationarity is present and meaningful, and that local variations in model parameters reflect real underlying processes rather than random noise. The method presumes that nearby observations are more relevant for explaining local relationships than distant ones, an assumption operationalized through the spatial weighting kernel and bandwidth selection. While this assumption is generally appropriate in urban socioeconomic analyses, it may oversimplify complex, multi-scalar processes that operate beyond immediate spatial neighborhoods.

• Additionally, GWR inherits the core assumptions of linear regression, including linearity, additivity, and independence of errors at the local scale. Although local calibration mitigates some forms of spatial autocorrelation, it does not fully eliminate the risk of residual spatial dependence, particularly in densely urbanized areas with strong structural patterns.

• Also we need to have into account that the analysis relies on cross-sectional data from different reference years, specifically the Purchasing Power Index from INE (2022) and the Gambling Stores census from the City of Madrid (2024). This temporal mismatch assumes relative stability in the spatial distribution of purchasing power over the short term. While this assumption is reasonable for aggregated socioeconomic indicators, it may obscure short-term dynamics or recent neighborhood-level changes.

The results of this study should be interpreted as associational rather than causal. GWR identifies spatially varying relationships between purchasing power and gambling store distribution, but it does not establish causal directionality. The observed patterns may reflect a combination of regulatory frameworks, commercial location strategies, historical land-use patterns, and unobserved socioeconomic factors.

Moreover, areas exhibiting strong local relationships should not be automatically interpreted as zones of direct vulnerability without complementary qualitative, behavioral, or health-related data. Gambling harm is a multidimensional phenomenon, and the presence of gambling establishments constitutes only one potential exposure factor.

Finally, this analysis focuses exclusively on the relationship between purchasing power and the spatial distribution of Gambling Stores. Other relevant dimensions of urban vulnerability—such as age structure, unemployment, educational attainment, or proximity to schools—are not explicitly modeled. As such, the results should be viewed as a partial and exploratory assessment of urban vulnerability, intended to inform further multivariate and multi-scalar analyses rather than provide a definitive evaluation

Anyway, my aim writing this post is start understanding this potentional multivariable correlation and this is only the first step. Hope you are still reading this and come back every now and then to keep reading 🙂

Sources:
https://datos.madrid.es/portal/site/egob/menuitem.c05c1f754a33a9fbe4b2e4b284f1a5a0/?vgnextoid=66665cde99be2410VgnVCM1000000b205a0aRCRD&vgnextchannel=374512b9ace9f310VgnVCM100000171f5a0aRCRD
https://livingatlas.arcgis.com/en/home/
https://www.txalaparta.eus/es/libros/ludomorfina?srsltid=AfmBOop4ZFCax6eeJt223I94jsH4iLDEKRtJT6Xlrhip7WuS7agtOowR
https://pro.arcgis.com/en/pro-app/3.4/tool-reference/spatial-statistics/how-geographicallyweightedregression-works.htm
https://www.publichealth.columbia.edu/research/population-health-methods/geographically-weighted-regression
https://www.sciencedirect.com/topics/earth-and-planetary-sciences/geographically-weighted-regression
https://carto.com/blog/how-geographically-weighted-regression-works

Alberto C.
GIS Analyst and ex-freelancer